Geometrie! Už se bojíte? Možná jste si právě vzpomněli na hodiny nezáživného rýsování a učení vzorečků. Což je škoda, protože geometrie je fascinující a krásná věda, kde všechno souvisí se vším – i když vám to možná učitelé neřekli. Vzájemné souvislosti jsou v geometrii téměř všude – my si ukážeme jednoduchou, ale elegantní ukázku, která k nám přišla až z dálek starověkého Řecka a středověké Arábie.
Měsíček Hippokratův
Pojďme vypočítat obsah fialového měsíčku, který vidíme na obrázku! Už při té představě se možná leckomu udělalo nevolno a hned vidí ty strany a strany odvozování, které k tomu budou určitě potřeba. Nebo že by nebyly?

Staří Řekové byli ve zdlouhavém odvozování mistry, tentokrát ale geometrovi jménem Hippokratés z Chiu (ne tomu s přísahou, ten byl lékařem a pocházel z ostrova Kós) stačilo jen docela kratičké. Tím zjistil, a hlavně dokázal, že obsah fialového měsíčku je stejný jako obsah zeleného pravoúhlého rovnoramenného trojúhelníku. A určit obsah trojúhelníku je přece snadné! Jenže jak na to přišel? Podívejme se na obrázek znovu, tentokrát bez barviček, ale zato s doplněnými čarami. A představme si přitom, jaké úvahy se starověkému geometrovi mohly honit hlavou.
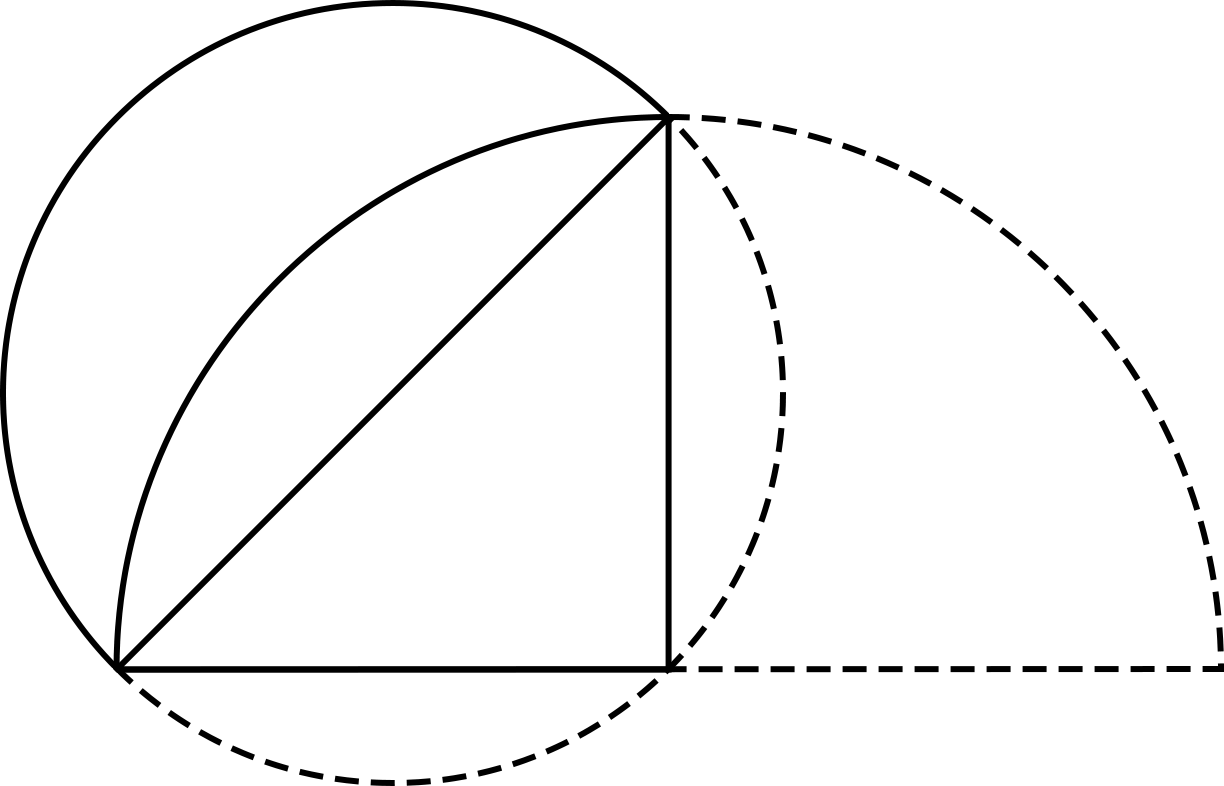
Hippokratés nad obrázkem dumá, až se důkladně podívá na úseč – plochu ve tvaru luku, která leží mezi trojúhelníkem a měsíčkem. Vidí, že plocha měsíčku společně s plochou úseče dá dohromady plochu menšího z půlkruhů, stejně jako plocha trojúhelníka s úsečí dá dohromady polovinu plochy toho většího.
Pak si vzpomene na svého předchůdce Pythagora a hned ví, že délka přepony trojúhelníka je √2-násobek délky jeho odvěsen. Plocha kruhu je úměrná druhé mocnině jeho průměru – a když si Hippokratés všechny ty poměry představí a důkladně promyslí, uvědomí si, že menší kruh má tím pádem poloviční plochu oproti tomu většímu.
Co to znamená? Znamená to, že menší půlkruh (měsíček + úseč) je stejně velký jako větší čtvrtkruh (trojúhelník + úseč). Teď už Hippokratovi stačí od obou útvarů odečíst plochu úseče. Tím potvrdí, že plocha měsíčku je stejně velká jako plocha trojúhelníku.
Dva měsíčky Alhazenovy
Pojďme ale dále, a to nejen v čase. Nějakých 900 let po Hippokratovi ukázal arabský učenec Hasan ibn al-Hajtham (Alhazen), že podobně to funguje, když jsou měsíčky u trojúhelníku hned dva.
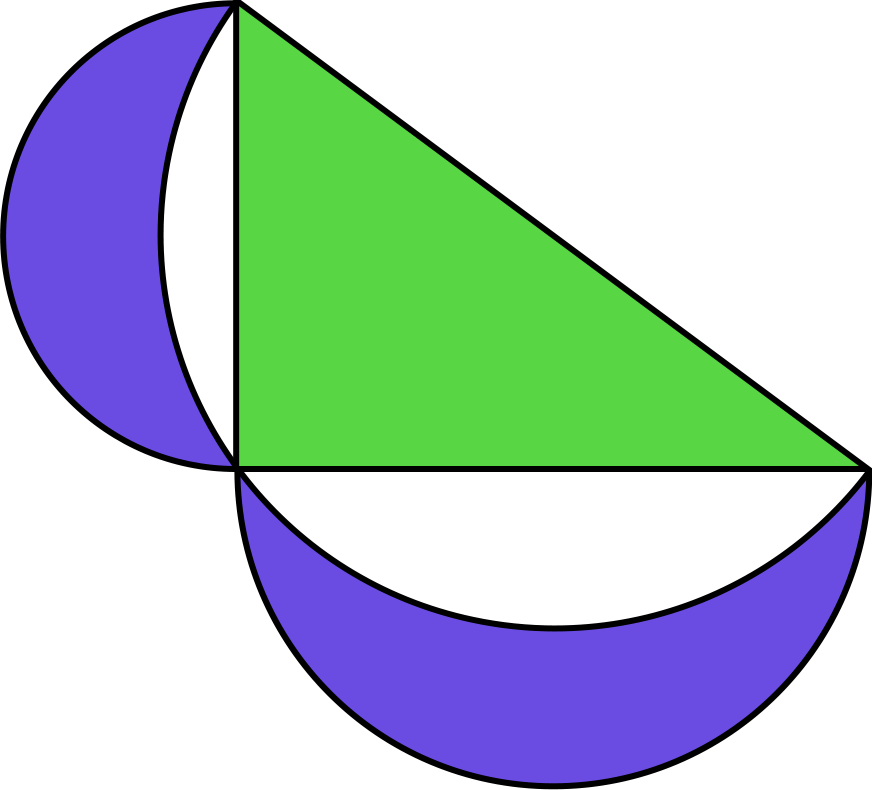
I tady platí, že fialová plocha, tedy oba měsíčky dohromady, mají stejnou plochu jako zelený pravoúhlý trojúhelník, který tentokrát ani nemusí být rovnoramenný. Podíváme se na schéma a vidíme, že al-Hajthamovy úvahy se mohly ubírat podobným směrem jako dříve Hippokratovy.
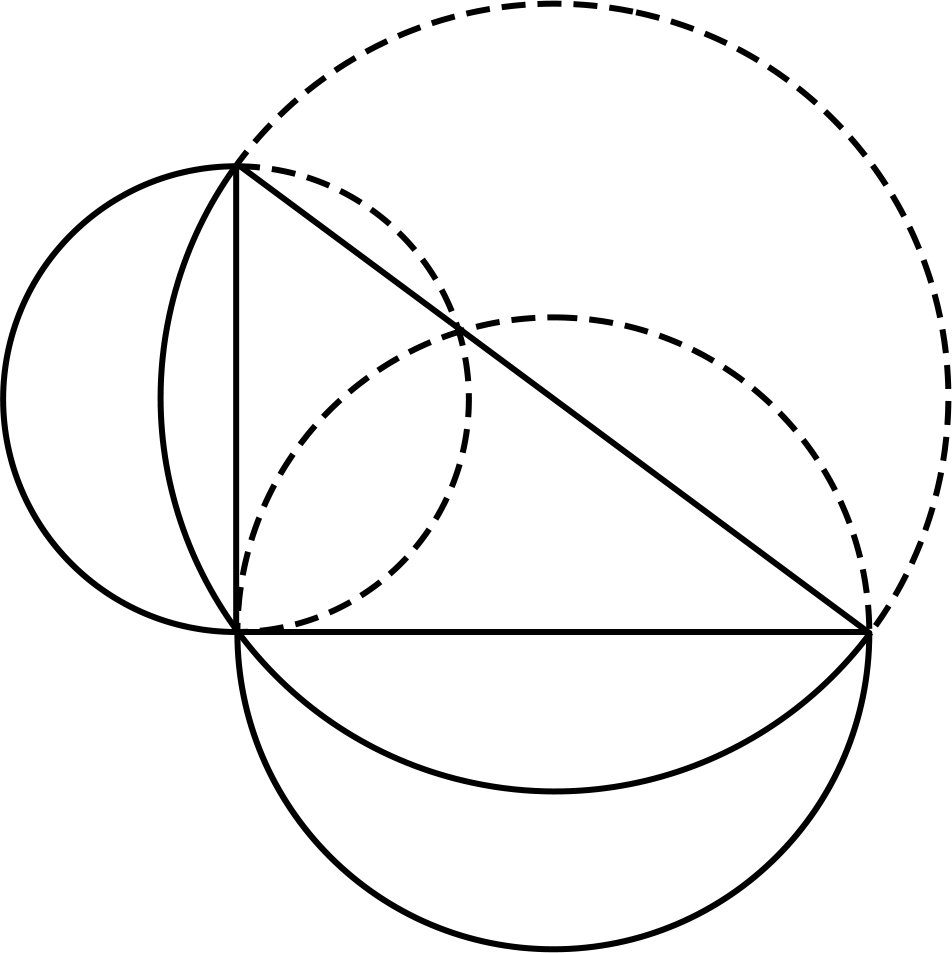
Zase jsou tu úseče mezi měsíčky a trojúhelníkem. A al-Hajtham vidí, že každý měsíček spolu se svou úsečí dávají dohromady půlkruh, stejně jako trojúhelník s oběma úsečemi dohromady. Určitě si taky rychle vzpomene na Pythagora – tenhle obrázek je přece podobný jeho slavné větě, jen místo čtverců jsou nad stranami trojúhelníku kruhy! To ale znamená, že dva menší půlkruhy (oba měsíčky + obě úseče), které jsou nad odvěsnami, jsou dohromady stejné velké jako ten nad přeponou (trojúhelník + obě úseče). Stejně jako Hippokratés tak může al-Hajtham úseče odečíst a najisto prohlásit, že plocha obou měsíčků dohromady je stejně velká jako plocha trojúhelníku.
A to se mělo dokázat!
Samozřejmě, že oba důkazy se dají vést exaktně, a přesně to si ukážeme v tomto odstavci pro fajnšmekry. Napřed si ale musíme zavést nějaké značení. Začněme Hippokratovým měsíčkem. Délku odvěsny trojúhelníku označíme r, plochu trojúhelníku T, plochu měsíčku M a plochu úseče mezi nimi U. Z Pythagorovy věty plyne, že délka přepony je √(2)r. Dále platí, že 2(T+U) = (πr²)/2, čehož T+U = πr²/4. Zároveň M+U = π(√(2)r/2)²/2 = πr²/4. Platí tedy rovnost T = M = πr²/4 – U.
Pro druhý případ označme delší odvěsnu trojúhelníku r, kratší odvěsnu s, přeponu t, větší měsíček M, větší úseč U, menší měsíček N a menší úseč V. Vidíme, že M+U = (πr²)/2, N+V = (πs²)/2 a T+U+V = (πt²)/2. Z Pythagorovy věty plyne, že t² = r²+s². Pokud celou rovnici vynásobíme konstantou π/2, dostaneme (πr²)/2+(πs²)/2 = (πt²)/2, a tedy M+U+N+V = T+U+V. Odečtením plochy obou úsečí získáme rovnost M+N = T.
Autorem obrázků je TondaMikaSan, děkujeme!
Zdroje k hlubšímu bádání:
- Hippokratova kvadratura měsíčků. In: Řecké matematické texty, Oikoymenh 2011, ISBN 80-7298-308-7.
- Lune of Hippocrates

